Open Optimization Library -- Reference Manual

This file documents the Open Optimization Library (OOL), a collection of numerical routines for optimization. It corresponds to release 0.2.0 of the library.

More information about OOL can be found at the project homepage, http://ool.sourceforge.net.

Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License.

1. Introduction

The Open Optimization Library (OOL) is a collection of routines for constrained minimization problems, implemented following the GNU Scientific Library (GSL) standards. The routines have been either translated into C or written from scratch in C, and present a modern Applications Programming Interface (API) for C programmers, allowing wrappers to be written for very high level languages. The source code is distributed under the GNU General Public License.

1.1 Routines available in OOL

The library aims to cover a wide range of methods in constrained optimization. Initially, routines are available for minimization of differentiable functions subject to simple bounds on their variables.

The use of these routines is described in this manual. Each chapter provides detailed definitions of the functions, followed by example programs and references to the articles on which the algorithms are based.

1.2 OOL is Free Software

Specifically, we want to make sure that you have the right to share copies of programs that you are given which use the Open Optimization Library, that you receive their source code or else can get it if you want it, that you can change these programs or use pieces of them in new free programs, and that you know you can do these things.

To make sure that everyone has such rights, we have to forbid you to deprive anyone else of these rights. For example, if you distribute copies of any code which uses the Open Optimization Library, you must give the recipients all the rights that you have received. You must make sure that they, too, receive or can get the source code, both to the library and the code which uses it. And you must tell them their rights. This means that the library should not be redistributed in proprietary programs.

Also, for our own protection, we must make certain that everyone finds out that there is no warranty for the Open Optimization Library. If these programs are modified by someone else and passed on, we want their recipients to know that what they have is not what we distributed, so that any problems introduced by others will not reflect on our reputation.

The precise conditions for the distribution of software related to the Open Optimization Library are found in the GNU General Public License (see section GNU General Public License). Further information about this license is available from the GNU Project webpage Frequently Asked Questions about the GNU GPL,

• http://www.gnu.org/copyleft/gpl-faq.html

1.3 Obtaining OOL

• http://ool.sourceforge.net/

1.4 No Warranty

1.5 Reporting Bugs

If you find a bug which is not listed in these files please report it to biloti@mat.ufpr.br.

All bug reports should include:

• The version number of OOL
• The version number of GSL
• The hardware and operating system
• The compiler used, including version number and compilation options
• A description of the bug behavior
• A short program which exercises the bug

2. Using the library

2.1 ANSI C Compliance

The library is written in ANSI C and is intended to conform to the ANSI C standard. It should be portable to any system with a working ANSI C compiler.

The library does not rely on any non-ANSI extensions in the interface it exports to the user. Programs you write using OOL can be ANSI compliant. Extensions which can be used in a way compatible with pure ANSI C are supported, however, via conditional compilation. This allows the library to take advantage of compiler extensions on those platforms which support them.

When an ANSI C feature is known to be broken on a particular system the library will exclude any related functions at compile-time. This should make it impossible to link a program that would use these functions and give incorrect results.

To avoid namespace conflicts all exported function names and variables have the prefix ool_, while exported macros have the prefix OOL_.

2.2 Compiling and Linking

#include <ool/ool_conmin.h>

If the directory is not installed on the standard search path of your compiler you will also need to provide its location to the preprocessor as a command line flag. The default location of the `ool' directory is `/usr/local/include/ool'. A typical compilation command for a source file `example.c' with the GNU C compiler gcc is,

gcc -I/usr/local/include -c example.c

The library is installed as a single file, `libool.a'. A shared version of the library is also installed on systems that support shared libraries. The default location of these files is `/usr/local/lib'. To link against the library you need to specify not only the main library, but also the GSL library, which is required by OOL, and a supporting CBLAS library, which provides standard basic linear algebra subroutines. A suitable CBLAS implementation is provided in the library `libgslcblas.a' if your system does not provide one. The following example shows how to link an application with the library,

gcc example.o -lool -lgsl -lgslcblas -lm

gcc example.o -lool -lgsl -lcblas -lm

gcc example.o -lool -lgsl -lcblas -latlas -lm

The program ool-config provides information on the local version of the library. For example, the following command shows that the library has been installed under the directory `/usr/local',

bash$ ool-config --prefix
/usr/local

2.3 Shared Libraries

LD_LIBRARY_PATH=/usr/local/lib:$LD_LIBRARY_PATH
export LD_LIBRARY_PATH
./example

setenv LD_LIBRARY_PATH /usr/local/lib:$LD_LIBRARY_PATH

To save retyping these commands each session they should be placed in an individual or system-wide login file.

To compile a statically linked version of the program, use the -static flag in gcc,

gcc -static example.o -lool -lgsl -lgslcblas -lm

2.4 Compatibility with C++

2.5 Aliasing of arrays

2.6 Thread-safety

The library can be used in multi-threaded programs. All the functions are thread-safe, in the sense that they do not use static variables. Memory is always associated with objects and not with functions. For functions which use workspace objects as temporary storage the workspaces should be allocated on a per-thread basis. For functions which use table objects as read-only memory the tables can be used by multiple threads simultaneously. Table arguments are always declared const in function prototypes, to indicate that they may be safely accessed by different threads.

3. Quick Start

To impatients, this chapter works out an example on the usage of the library. The code presented, despite its simplicity, can be used to solve real problems with minor modifications.

3.1 Example

Consider the problem

We present a sample code for solving this problem with help of the OOL, and comment it line by line.

   1: #include <stdio.h>
   2: #include <ool/ool_conmin.h>

   3: void iteration_echo( ool_conmin_minimizer *M );

Line 1 includes the C standard IO header and line 2 includes the header for the OOL library. The last should be included in every program that uses OOL. Line 3 simply defines the prototype of an auxiliary function defined below. The following block defines the objective function. The prototype for objective function should always be like in line 4 and 5. The objective function may have parameters, which are provided by a void pointer params. In this example params points to a vector. To be used inside the function, params is typecasted to gsl_vector * (line 7). For functions depending on several parameters, params could points to a structure defined to cluster them all.

   4: double
   5: fun( const gsl_vector *X, void* params )
   6: {
   7:    gsl_vector *a = (gsl_vector *) params;
   8:    size_t ii, nn;
   9:    double ai, xi;
  10:    double f;

  11:    nn = X->size;

  12:    f = 0;
  13:    for( ii = 0; ii < nn; ii++ )
  14:       {
  15:          ai = gsl_vector_get( a, ii );
  16:          xi = gsl_vector_get( X, ii );
  17:          f += (xi - ai)*(xi - ai);
  18:       }
  19:    return f;
  20: }

The next block implements functions to evaluate the gradient (lines 21--35), objective function and gradient (simultaneously) (36--53), and the product of Hessian by a given vector (54--66).

  21: void
  22: fun_df( const gsl_vector *X, void* params, gsl_vector *G )
  23: {
  24:    gsl_vector *a = (gsl_vector *) params;
  25:    size_t ii, nn;
  26:    double ai, xi, gi;

  27:    nn = X->size;

  28:    for( ii = 0; ii < nn; ii++ )
  29:       {
  30:          ai = gsl_vector_get( a, ii );
  31:          xi = gsl_vector_get( X, ii );
  32:          gi = 2 * ( xi - ai );
  33:          gsl_vector_set( G, ii, gi );
  34:       }
  35: }

  36: void
  37: fun_fdf( const gsl_vector *X, void* params,
  38:          double *f, gsl_vector *G )
  39: {
  40:    gsl_vector *a = (gsl_vector *) params;
  41:    size_t ii, nn;
  42:    double ai, xi, gi;

  43:    nn = X->size;
  44:    (*f) = 0;

  45:    for( ii = 0; ii < nn; ii++ )
  46:       {
  47:          ai = gsl_vector_get( a, ii );
  48:          xi = gsl_vector_get( X, ii );
  49:          (*f) += (xi - ai)*(xi - ai);
  50:          gi = 2 * ( xi - ai );
  51:          gsl_vector_set( G, ii, gi );
  52:       }
  53: }

  54: void
  55: fun_Hv( const gsl_vector *X, void *params,
  56:         const gsl_vector *V, gsl_vector *hv )
  57: {
  58:    size_t ii, nn;
  59:    double hvi;

  60:    nn = X->size;

  61:    for( ii = 0; ii < nn; ii++ )
  62:       {
  63:          hvi = 2 * gsl_vector_get( V, ii );
  64:          gsl_vector_set( hv, ii, hvi);
  65:       }
  66: }

Finally, comes the main routine which drives the optimization. Lines 69 and 70 define the number of variables of the problem and the limit for the number of iterations, respectively.

  67: int main( void )
  68: {
  69:   size_t nn   = 100;
  70:   size_t nmax = 10000;
  71:   size_t ii;
  72:   int status;

The next two lines are the only two lines which are method dependent. They are responsible to select which optimization algorithm will be used, the SPG algorithm, in this example.

  73:   const ool_conmin_minimizer_type *T = ool_conmin_minimizer_spg;
  74:   ool_conmin_spg_parameters P;

The next four lines declare variables to hold the objective function, the constraints, the minimizer method, and the initial iterate, respectively.

  75:   ool_conmin_function   F;
  76:   ool_conmin_constraint C;
  77:   ool_conmin_minimizer *M;
  78:   gsl_vector *X;

In line 79 a vector is declared to represent the function parameters as in the description of the problem. In the following block, this vector is initialized as a = (0.1, 0.2,..., 10)^T.

  79:   gsl_vector *a;

  80:   a = gsl_vector_alloc( nn );
  81:   for ( ii = 0; ii < nn; ii++)
  82:      gsl_vector_set( a, ii, ((double) ii + 1.0)/10.0 );

The function structure is filled in with the number of variables (line 83), pointers to routines to evaluate the objective function and its derivatives (84--87), and a pointer to the function parameters (88).

  83:   F.n   = nn;
  84:   F.f   = &fun;
  85:   F.df  = &fun_df;
  86:   F.fdf = &fun_fdf;
  87:   F.Hv  = &fun_Hv;
  88:   F.params = (void *) a;

The memory allocation to store the bounds is performed in lines 90 and 91. Further the lower and upper bounds are set to -3 and 3, respectively, to all variables.

  89:   C.n = nn;
  90:   C.L = gsl_vector_alloc( C.n );
  91:   C.U = gsl_vector_alloc( C.n );

  92:   gsl_vector_set_all( C.L, -3.0 );
  93:   gsl_vector_set_all( C.U,  3.0 );

These two lines allocate and set the initial iterate.

  94:   X = gsl_vector_alloc( nn );
  95:   gsl_vector_set_all( X, 1.0 );

Line 96 allocate the necessary memory for an instance of the optimization algorithm of type T (defined in line 73). Line 97 initializes its parameters to default values. If the you want to tune the method by changing the default values to some parameter this should be done between lines 97 and 98.

  96:   M = ool_conmin_minimizer_alloc( T, nn );

  97:   ool_conmin_parameters_default( T, (void*)(&P) );

In line 98, everything is put together. It states that this instance of the method M is responsible for minimizing function F, subject to constraints C, starting from point X, with parameters P.

  98:   ool_conmin_minimizer_set( M, &F, &C, X, (void*)(&P) );

We are now in position to begin iterating. The iteration counter is initialized (line 99) and some information concerning the initial point is displayed (101--102). The iteration loop is repeated while the maximum number of iterations was not reached and the status is OOL_CONTINUE. Further conditions could also be considered (maximum number of function/gradient evaluation for example). The iteration counter is incremented (104) and one single iteration of the method is performed (105). In line 106 the current iterate is checked for optimality. Finally some information concerning this iteration is displayed.

  99:   ii = 0;
 100:   status = OOL_CONTINUE;

 101:   printf( "%4i : ", ii );
 102:   iteration_echo ( M );

 103:   while( ii < nmax && status == OOL_CONTINUE ){
 104:      ii++;
 105:      ool_conmin_minimizer_iterate( M );
 106:      status = ool_conmin_is_optimal( M );

 107:      printf( "%4i : ", ii );
 108:      iteration_echo( M );
 109:   }

The program ends displaying the convergence status (110--113), number of variables, function and gradient evaluations, the objective function value at the last iterate and the norm of its projected gradient (114--123).

 110:   if(status == OOL_SUCCESS)
 111:      printf("\nConvergence in %i iterations", ii);
 112:   else
 113:      printf("\nStopped with %i iterations", ii);

 114:   printf("\nvariables................: %6i"
 115: 	 "\nfunction evaluations.....: %6i"
 116: 	 "\ngradient evaluations.....: %6i"
 117: 	 "\nfunction value...........: % .6e"
 118: 	 "\nprojected gradient norm..: % .6e\n",
 119: 	 nn,
 120: 	 ool_conmin_minimizer_fcount( M ),
 121: 	 ool_conmin_minimizer_gcount( M ),
 122: 	 ool_conmin_minimizer_minimum( M ),
 123: 	 ool_conmin_minimizer_size( M ));

To finalize, all allocated memory is freed.

 124:   gsl_vector_free( C.L );
 125:   gsl_vector_free( C.U );
 126:   gsl_vector_free( X );
 127:   gsl_vector_free( a );

 128:   ool_conmin_minimizer_free( M );

 129:   return OOL_SUCCESS;
 130: }

This last block codes an auxiliar function to display few elements of the current iterate and the objective value.

 131: void iteration_echo( ool_conmin_minimizer *M )
 132: {
 133:   double f = M->f;
 134:   size_t ii, nn;

 135:   nn = X->size;

 136:   printf( "f( " );
 137:   for( ii = 0; ii < 3; ii++ )
 138:     printf( "%+6.3e, ", gsl_vector_get( M->x, ii ) );
 139:   printf( "... ) = %+6.3e\n", f );

 140: }

This code produces the output:

   0 : f( +0.000e+00, +0.000e+00, +0.000e+00, ... ) = +3.384e+03
   1 : f( +1.000e-02, +2.000e-02, +3.000e-02, ... ) = +2.741e+03
   2 : f( +1.000e-01, +2.000e-01, +3.000e-01, ... ) = +1.168e+03

Convergence in 2 iterations
variables................:    100
function evaluations.....:      3
gradient evaluations.....:      3
function value...........:  1.167950e+03
projected gradient norm..:  8.881784e-16

4. Brief Theoretical Introduction

This chapter furnishes a brief description of the theory regarding constrained minimization.

4.1 Theory Overview

The problem considered in the CONMIN library is the minimization of a smooth function ƒ: Rⁿ → R subject to x ∈ Ω. The set Ω defined by the constraints is called feasile set. Briefly, our aim is to solve

min ƒ(x), s.t. x ∈ Ω

where, by this, we mean to find a local minimizer, that is, a point x^∗ such that

ƒ(x^∗) ≤ ƒ(x), for all x ∈ Ω near x^∗.

4.2 Optimality Conditions

The most general situation for the feasible set is when

Ω = { x ∈ Rⁿ | g(x) &le 0, h(x) = 0, L ≤ x &le U }.

where g:Rⁿ → R^ng and h:Rⁿ → R^nh. In this case, the Karush-Kuhn-Tucker (KKT) first order optimality conditions states that, if x^∗ is a local minimum, then there exist λ_i, for i = 1,…n_h and μ_i, for i = 1,…n_g, such that

We say that x^∗ is a critical point if x^∗ solves the system above. Therefore, the critical points are candidates for the local minimum.

4.2.1 Convex Case

Instead of finding the critical points by solving the KKT system above, methods for minimization subject to general constraints often may be built based on combinations of methods for minimization with simpler constraints. For instance, when Ω is convex and ƒ is a smooth function, the necessary optimality condition is that the projected gradient given by

g_p = P_Ω (x - ∇ ƒ(x) ) - x.

vanishes at the minimum, where P_Ω is the ortogonal projection onto Ω. This can be seen as a particular form of the KKT optimality conditions. The critical points x^∗, in this case, are those such that g_p(x^∗) = 0.

4.2.2 Box Constraints

The simplest convex case, regarding the constraints, is when the feasible set Ω is given by

Ω = { x ∈ Rⁿ | L ≤ x &le U }.

We say that the minimization is subject to bound, simple bound or box constraints. Note that the projection onto the feasible set is simply a box projection, and is given by

(P_Ω(x))_i = min{ max{ L_i, x_i }, U_i }.

4.3 General Method Structure

4.3.1 Line Search

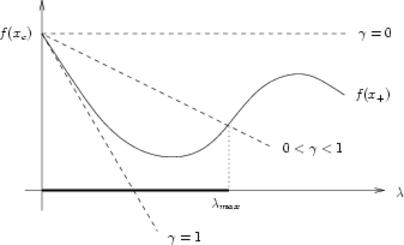
A common component of optimization methods are line search strategies. By this we mean that once given the current point x_c, and a descent direction d, we look for λ such that

ƒ(x_c + λ d) &le ƒ(x_c).

ƒ(x_c + λ d) ≤ ƒ(x_c) + λ γ ∇ƒ(x_c)^T d,

ƒ(x₊) ≤ ƒ(x_c) + γ ∇ƒ(x_c)^T (x₊ - x_c),

The nonmonotone Armijo condition to accept a trial point x₊ is

ƒ(x₊) ≤ max_{0 ≤ j ≤ min{ k, M-1}} ƒ(x_k-j) + γ ∇ƒ(x_k)^T (x₊ - x_k),

λ ← max{ σ₁ λ, min{ σ₂ λ, &lambda^∗ } }

4.4 References and Further Reading

• D.P. Bertsekas, Nonlinear Programming, Athena Scientific, 1999.

• D.P. Bertsekas, Constrained Optimization and Lagrange Multiplier Methods, Athena Scientific, 1982.

• R. Fletcher, Practical Methods for Optimization, John Wiley and Sons, 2nd ed., 1987.

• C.T. Kelley, Iterative Methods for Optimization, Frontiers in Applied Mathematics, SIAM, Philadelphia, 1999.

5. Constrained Optimization

This chapter describes the common interfaces for constrained minimization of arbitrary multidimensional functions. The library provides implementations and reimplementations of methods published in well known optimization and applied mathematics journals. The library follows, as close as possible, the GSL standards and tries to use the GSL routines, specially those ones for optimization, described at chapters 31, 32, 33, 34, 35 and 36 of the GSL Reference Manual, version 1.4.

In order to fit the same standards of the GSL multidimensional minimization, only one iteration, for each method, is implemented. This means that in case of reimplemented codes, to obtain the same results of the original version, the user must provide a main routine that calls the OOL method and checks for optimality, as well as for stopping criteria, exactly as in the original implementation.

The header file `ool_conmin.h' contains prototypes for the minimization functions and related declarations.

5.1 Choosing the Minimization Method

Initially the user must define two variables: T indicates the method used and P stands for its parameters. For example, if you choose to use the Projected Gradient Methods (pgrad), the code lines are

  /* Method structs */
  const ool_conmin_minimizer_type *T = ool_conmin_minimizer_pgrad;
  ool_conmin_pgrad_parameters P;

5.2 Initialization and Finalization

The following function initializes a multidimensional constrained minimizer. The minimizer itself depends only on the dimension of the problem and the algorithm and can be reused for different problems.

Function: ool_conmin_minimizer * ool_conmin_minimizer_alloc (const ool_conmin_minimizer_type *T, size_t n)

This function returns a pointer to a newly allocated instance of a minimizer of type T for an n-dimension function. If there is insufficient memory to create the minimizer then the function returns a null pointer and the error handler is invoked with an error code of OOL_ENOMEM.

Function: void ool_conmin_parameters_default (const ool_conmin_minimizer_type * T, void * P)

This function initializes the parameters P with its default values, for algorithm T.

Function: int ool_conmin_minimizer_set (ool_conmin_minimizer * M, ool_conmin_function *fdf, ool_conmin_constraint * C, const gsl_vector * x, void * P)

This function initializes the minimizer M to minimize the function fdf subject to the constraints C, starting from the initial point x. The parameters for the method M are given in P. Note that for some methods, the initial point x must be feasible.

Function: void ool_conmin_minimizer_free (ool_conmin_

minimizer *M) This function frees all the memory associated to the minimizer M.

Function: const char * ool_conmin_minimizer_name (const ool_conmin_minimizer * M)

This function returns a pointer to the name of the minimizer. For example,

printf ("s is a '%s' minimizer\n", ool_conmin_minimizer_name (s));

would print something like s is a 'pgrad' minimizer.

5.3 Providing a function to minimize

You must provide a parametric function of variables for the minimizer to operate on. You may also need to provide a routine which calculates the gradient of the function and a third routine which calculates both the function value and the gradient together. Some methods may require a routine to calculate the Hessian times a given vector. In order to allow for general parameters the functions are defined by the following data type:

Data Type: ool_conmin_function

This data type defines a general function of variables with parameters and the corresponding gradient vector of derivatives, as well as the product of the Hessian matrix by a vector.

size_t n

the dimension of the system, i.e. the number of components of the vectors x.

double (* f) (const gsl_vector * x, const void * params)

This function should return the result for argument x and parameters params.

void (* df) (const gsl_vector * x, const void * params, gsl_vector * g)

This function should store the n-dimensional gradient ) / \partial x_i} in the vector g for argument x and parameters params, returning an appropriate error code if the function cannot be computed.

void (* fdf) (const gsl_vector * x, const void * params, double * f, gsl_vector * g)

This function should set the values of the f and g as above, for arguments x and parameters params. This function provides an optimization of the separate functions for and -- it is always faster to compute the function and its gradient at the same time.

void (* Hv) (const gsl_vector *x, const void * params, const gsl_vector * V, gsl_vector * hv )

This function should return the value hv of the Hessian matrix times the vector v, for arguments x and parameters params. For some methods, this routine may be required.

void * params

A pointer to the parameters of the function.

double
quadratic( const gsl_vector *X, void* params )
{
  size_t ii, nn;
  double f, x;

  nn = X->size;

  f = 0;

  for( ii = 0; ii < nn; ii++ )
    {
      x  = gsl_vector_get( X, ii );
      f += (ii+1) * gsl_pow_2( x );
    }

  return f;
}

void
quadratic_df( const gsl_vector *X, void* params, gsl_vector *G )
{
  size_t ii, nn;
  double xx, gg;

  nn = X->size;

  for( ii = 0; ii < nn; ii++ )
    {
      xx = gsl_vector_get( X, ii );
      gg = 2.0 * (ii+1) * xx;
      gsl_vector_set( G, ii, gg );
    }
}

void
quadratic_fdf( const gsl_vector *X, void* params,
	       double *f, gsl_vector *G )
{
  size_t ii, ip1, nn;
  double xx, gg;

  nn = X->size;
  (*f) = 0;

  for( ii = 0; ii < nn; ii++ )
    {
      ip1 = ii + 1;

      xx = gsl_vector_get( X, ii );

      (*f) += ip1 * gsl_pow_2( xx );
      gg = 2.0 * ip1 * xx;

      gsl_vector_set( G, ii, gg );
    }
}

void
quadratic_Hv( const gsl_vector *X, void *params,
	      const gsl_vector *V, gsl_vector *hv )
{
  size_t ii, nn;
  double aux;

  nn = X->size;

  for( ii = 0; ii < nn; ii++ )
    {
      aux = 2.0 * (ii+1) * gsl_vector_get( V, ii );
      gsl_vector_set( hv, ii, aux );
    }
}

The function structure can be initialized using the following code,

 ool_conmin_function F;

 F.n   = nn;
 F.f   = &quadratic;
 F.df  = &quadratic_df;
 F.fdf = &quadratic_fdf;
 F.Hv  = &quadratic_Hv;
 F.params = NULL;

5.4 Providing the constraints

You must provide the lower and upper bound of the box constraints for the minimizers to operate on.

Data Type: ool_conmin_constraint

This data type defines a general simple bound constraints for variables.

size_t n

the dimension of the system, i.e. the number of components of the vectors x.

gsl_vector * L

gsl_vector * U

box constraints.

The constraints can be initialized using the following code,

 ool_conmin_constraint  C;
 C.n  = nn;

 C.L = gsl_vector_alloc( nn );
 C.U = gsl_vector_alloc( nn );

 gsl_vector_set_all( C.L,   1.0 );
 gsl_vector_set_all( C.U,  10.0 );

5.5 Iteration

The following function drives the iteration of each algorithm. The function performs one iteration to update the state of the minimizer. The same function works for all minimizers so that different methods can be substituted at runtime without modifications to the code.

Function: int ool_conmin_minimizer_iterate (ool_conmin_minimizer *M)

The function performs a single iteration of the minimizer M. If the iteration encounters an unexpected problem then an error code will be returned.

Function: int ool_conmin_minimizer_restart (ool_conmin_minimizer *M)

This function resets the minimizer M to use the current point as a new starting point.

The method parameters can be changed between the iterations, using the functions

Function: void ool_conmin_parameters_get (const ool_conmin_minimizer *M, void *param_view)

Function: int ool_conmin_parameters_set (ool_conmin_minimizer *M, void *new_param)

The first one returns the parameters param_view used in the previous iteration, and the second one sets the new parameters new_param.

The minimizer maintains a current best estimate of the minimum at all times. This information can be accessed through the following auxiliary functions,

Function: gsl_vector * ool_conmin_minimizer_x (const ool_conmin_minimizer * M)

Function: @deftypefunx{gsl_vector *} ool_conmin_minimizer_dx (const ool_conmin_minimizer * M)

Function: double ool_conmin_minimizer_minimum (const ool_conmin_minimizer * M)

Function: gsl_vector * ool_conmin_minimizer_gradient (const ool_conmin_minimizer * M)

Function: double ool_conmin_minimizer_size (const ool_conmin_minimizer * M)

These functions return the current best estimate of the location of the minimum, the last step, the value of the function at that point, its gradient, and minimizer specific characteristic size for the minimizer M, respectively.

5.6 Stopping Criteria

A minimization procedure should stop when one of the following conditions is true:

• A minimum has been found to within the user-specified precision.

• An error has occurred.

The handling of these conditions is under user control. The functions below permit the user to test the precision of the current result.

Function: int ool_conmin_is_optimal (ool_conmin_minimizer * M)

This functions checks for optimality and is method dependent. The test returns OOL_SUCCESS if the following condition is achieved, and OOL_CONTINUE otherwise.

Function: size_t ool_conmin_minimizer_fcount (const ool_conmin_minimizer * M)

Function: size_t ool_conmin_minimizer_gcount (const ool_conmin_minimizer * M)

Function: size_t ool_conmin_minimizer_hcount (const ool_conmin_minimizer * M)

These functions return, respectively, the number of objective function, gradient and product Hessian-vector evaluations.

5.7 Algorithms

Presently, there are only algorithms for simple bound constraints. They use the value of the function and most of its gradient at each evaluation point, too.

Minimizer: ool_conmin_minimizer_pgrad

This is a natural extension of the steepest descent algorithm to bound constraints problems. In each step, a line search is perfomed along the projected gradient direction.

Minimizer: ool_conmin_minimizer_spg

This is the classical projected gradient method extended to a include nonmonotone line search strategy and the spectral steplength, which greatly improves the convergence rate of the method.

Minimizer: ool_conmin_minimizer_gencan

This is a active-set method for smooth box-constrained minimization. The algorithm combines an unconstrained method, including a line search which aims to add many constraints to the working set at a single iteration, with a technique (spectral projected gradient) for dropping constraints from the working set.

5.8 References and Further Reading

• D.P. Bertsekas, Nonlinear Programming, Athena Scientific, 1999.

• D.P. Bertsekas, Constrained Optimization and Lagrange Multiplier Methods, Athena Scientific, 1982.

• R. Fletcher, Practical Methods for Optimization, John Wiley and Sons, 1987.

• C.T. Kelley, Iterative Methods for Optimization, Frontiers in Applied Mathematics, SIAM, 1999.

6. Projected Gradient Method

This chapter describes the routine PGRAD, for constrained minimization of differentiable multidimensional functions, which implements the Projected Gradient Method.

6.1 Overview

The problem solved by PGRAD is the minimization of a smooth function with bounds on the variables (see section 4. Brief Theoretical Introduction and 4.2.2 Box Constraints).

The Projected Gradient method is a natural extension of the Steepest Descent method for unconstrained minimization. At each step a line search is performed over direction of projected gradient. This method is not inteded to be used for production. For further details, see the reference at the end of this section.

6.2 Parameters

Inside PGRAD, there are few parameters which can be choosen to improve the minimizing efforts. The parameter list, together with the default values are given below.

Parameter: double tol = 1.0e-4

Tolerance on infinite norm of the projected gradient for optimality check.

Parameter: double fmin = -1e+99

Value to declare as unbounded.

Parameter: double alpha = 1.0e-4

Constant for the sufficient decrease condition

Parameter: double sigma1 = 0.1

Parameter: double sigma2 = 0.9

Bounds to the redution of the steplength.

6.3 Stopping Criteria

The algorithm declares convergence whenever the infinite norm of projected gradient is less than or equal to a given tolerance.

The infinite norm of the projected gradient at the current iterate can be retrieved by calling ool_conmin_minimizer_size() function.

6.4 Example

For an example of PGRAD, see section 3. Quick Start, replacing lines 73 and 75 of that code by

  const ool_conmin_minimizer_type *T = ool_conmin_minimizer_pgrad;
  ool_conmin_pgrad_parameters P;

The output of the program is shown below.

   0 : f( +0.000e+00, +0.000e+00, +0.000e+00, ... ) = +3.384e+03
   1 : f( +2.000e-01, +4.000e-01, +6.000e-01, ... ) = +1.190e+03
   2 : f( +1.800e-01, +3.600e-01, +5.400e-01, ... ) = +1.182e+03
   3 : f( +1.640e-01, +3.280e-01, +4.920e-01, ... ) = +1.177e+03
   4 : f( +1.512e-01, +3.024e-01, +4.536e-01, ... ) = +1.174e+03
   5 : f( +1.410e-01, +2.819e-01, +4.229e-01, ... ) = +1.172e+03
   6 : f( +1.328e-01, +2.655e-01, +3.983e-01, ... ) = +1.170e+03
   7 : f( +1.262e-01, +2.524e-01, +3.786e-01, ... ) = +1.169e+03
   8 : f( +1.210e-01, +2.419e-01, +3.629e-01, ... ) = +1.169e+03
   9 : f( +1.168e-01, +2.336e-01, +3.503e-01, ... ) = +1.169e+03
  10 : f( +1.134e-01, +2.268e-01, +3.403e-01, ... ) = +1.168e+03
  11 : f( +1.107e-01, +2.215e-01, +3.322e-01, ... ) = +1.168e+03
  12 : f( +1.086e-01, +2.172e-01, +3.258e-01, ... ) = +1.168e+03
  13 : f( +1.069e-01, +2.137e-01, +3.206e-01, ... ) = +1.168e+03
  14 : f( +1.055e-01, +2.110e-01, +3.165e-01, ... ) = +1.168e+03
  15 : f( +1.044e-01, +2.088e-01, +3.132e-01, ... ) = +1.168e+03
  16 : f( +1.035e-01, +2.070e-01, +3.106e-01, ... ) = +1.168e+03
  17 : f( +1.028e-01, +2.056e-01, +3.084e-01, ... ) = +1.168e+03
  18 : f( +1.023e-01, +2.045e-01, +3.068e-01, ... ) = +1.168e+03
  19 : f( +1.018e-01, +2.036e-01, +3.054e-01, ... ) = +1.168e+03
  20 : f( +1.014e-01, +2.029e-01, +3.043e-01, ... ) = +1.168e+03
  21 : f( +1.012e-01, +2.023e-01, +3.035e-01, ... ) = +1.168e+03
  22 : f( +1.009e-01, +2.018e-01, +3.028e-01, ... ) = +1.168e+03
  23 : f( +1.007e-01, +2.015e-01, +3.022e-01, ... ) = +1.168e+03
  24 : f( +1.006e-01, +2.012e-01, +3.018e-01, ... ) = +1.168e+03
  25 : f( +1.005e-01, +2.009e-01, +3.014e-01, ... ) = +1.168e+03
  26 : f( +1.004e-01, +2.008e-01, +3.011e-01, ... ) = +1.168e+03
  27 : f( +1.003e-01, +2.006e-01, +3.009e-01, ... ) = +1.168e+03
  28 : f( +1.002e-01, +2.005e-01, +3.007e-01, ... ) = +1.168e+03
  29 : f( +1.002e-01, +2.004e-01, +3.006e-01, ... ) = +1.168e+03
  30 : f( +1.002e-01, +2.003e-01, +3.005e-01, ... ) = +1.168e+03
  31 : f( +1.001e-01, +2.002e-01, +3.004e-01, ... ) = +1.168e+03
  32 : f( +1.001e-01, +2.002e-01, +3.003e-01, ... ) = +1.168e+03
  33 : f( +1.001e-01, +2.002e-01, +3.002e-01, ... ) = +1.168e+03
  34 : f( +1.001e-01, +2.001e-01, +3.002e-01, ... ) = +1.168e+03
  35 : f( +1.001e-01, +2.001e-01, +3.002e-01, ... ) = +1.168e+03
  36 : f( +1.000e-01, +2.001e-01, +3.001e-01, ... ) = +1.168e+03
  37 : f( +1.000e-01, +2.001e-01, +3.001e-01, ... ) = +1.168e+03
  38 : f( +1.000e-01, +2.001e-01, +3.001e-01, ... ) = +1.168e+03
  39 : f( +1.000e-01, +2.000e-01, +3.001e-01, ... ) = +1.168e+03
  40 : f( +1.000e-01, +2.000e-01, +3.000e-01, ... ) = +1.168e+03
  41 : f( +1.000e-01, +2.000e-01, +3.000e-01, ... ) = +1.168e+03
  42 : f( +1.000e-01, +2.000e-01, +3.000e-01, ... ) = +1.168e+03
  43 : f( +1.000e-01, +2.000e-01, +3.000e-01, ... ) = +1.168e+03
  44 : f( +1.000e-01, +2.000e-01, +3.000e-01, ... ) = +1.168e+03
  45 : f( +1.000e-01, +2.000e-01, +3.000e-01, ... ) = +1.168e+03
  46 : f( +1.000e-01, +2.000e-01, +3.000e-01, ... ) = +1.168e+03
  47 : f( +1.000e-01, +2.000e-01, +3.000e-01, ... ) = +1.168e+03
  48 : f( +1.000e-01, +2.000e-01, +3.000e-01, ... ) = +1.168e+03

Convergence in 48 iterations
variables................:    100
function evaluations.....:     96
gradient evaluations.....:     49
function value...........:  1.167950e+03
projected gradient norm..:  8.362779e-05

6.5 References and Further Reading

• C. T. Kelley, Iterative Methods of Optimization, SIAM, Philadelphia, 1999.

7. Spectral Projected Gradient Method

This chapter describes the routine SPG for constrained minimization of differentiable multidimensional functions on convex sets.

7.1 Overview

The Spectral Projected Gradient Method is designed to minimize differentiable function on convex sets. The SPG Method is similar to the Projected Gradient Method, differing only by the choice of the spectral steplength, which accelerates the convergence of the method. Despite this similarity, it can be shown that the SPG Method is related to the quasi-Newton family of methods.

This implementation deals with box constrained (see section 4. Brief Theoretical Introduction and 4.2.2 Box Constraints).

The SPG routine implements the version SPG2 of the Nonmonotone Spectral Projected Gradient Method, as published in Birgin et al. (2000), which differs from the classical SPG method by the nonmonotone Armijo sufficient decrease condition to accept a trial point (see section 4.3.1 Line Search). This method is a competitive option for large problems, since it has low memory requirements.

7.2 Parameters

Inside SPG, there is a set of parameters which can be changed to improve the minimizing efforts. The parameter list, together with the default values are given below.

Parameter: double fmin = -1.0e+99

Value to declare as unbounded.

Parameter: double tol = -1.0e-4

Tolerance on the infinite norm of the projected gradient to declare convergence.

Parameter: size_t M = 10

Nonmonotonicity parameter. Setting M to 1 turns the method monotone.

Parameter: double alphamax = 1.0e+30

Upper bound to spectral step size.

Parameter: double alphamin = 1.0e-30

Lower bound to spectral step size.

Parameter: double gamma = 1.0e-4

Sufficient decrease parameter ().

Parameter: double sigma1 = 0.1

Parameter: double sigma2 = 0.9

Bounds to the redution of the steplength.

7.3 Stopping Criteria

The method declares convergence whenever the function value is equal to or less than a prescribed value, through the fmin parameter, or the inifinte norm of projected gradient is less than the tolerance defined in tol parameter.

The infinite norm of the projected gradient at the current iterate can be retrieved by calling ool_conmin_minimizer_size() function.

7.4 Example

See section 3. Quick Start, for an example program which employs SPG.

7.5 References and Further Reading

• E.G. Birgin, J.M. Mart'{i}nez, and M. Raydan, Nonmonotone Spectral Projected Gradient Methods on Convex Sets, SIAM Journal on Optimization 10:1196--1211, 2000.

8. Gencan Method

This chapter describes the routine GENCAN for constrained minimization of arbitrary multidimensional functions.

8.1 Overview

The problem solved by GENCAN is the minimization of a smooth function with bounds on the variables (see section 4. Brief Theoretical Introduction and 4.2.2 Box Constraints).

Suppose that an iterate is inside a given face of (the feasible set) and consider to be the projection of inside this face. The main algorithm then performs the test , where . If false, the new point must remain in the face and an iteration of a truncated Newton method is performed (only for the free variables). However, if that condition holds, some constraint must be abandoned and the new point is computed doing one iteration of the "Spectral Projected Gradient" method. For further details, see the reference at the end of this section.

8.2 Parameters

Inside GENCAN, there is a set of parameters which can be changed to improve the minimizing efforts. The parameter list, together with the default values are given below.

Parameter: double epsgpen = 1.0e-5

Tolerance on euclidean norm of the projected gradient to declare convergence.

Parameter: double epsgpsn = 1.0e-5

Tolerance on infinite norm of the projected gradient to declare convergence.

Parameter: double fmin = -1.0e+99

Function value to declare as unbounded.

Parameter: double udelta0 = -1

Initial trust-region radius for Conjugate Gradient subalgorithm. The default value max(delmin, 0.1 max( 1, )) is used if udelta0 is non-positive.

Parameter: int ucgmia = -1

Parameter: int ucgmib = -1

Maximum number of iterations allowed for each call of the Conjugate Gradient subalgorithm. If ucgmia and ucgmib are both set to positive values, the maximum number of iterations is set as max(1, ucgmia * nind + ucgmib), where nind states for the number of variables of the subproblem. Otherwise, thr default value for the maximum number of iterations is a linear function of the infinite norm of the projected gradient, which ranges from max(1, 10 * log(nind)) to nind, as the current iterate gets closer to the solution.

Parameter: int cg_scre = 1

Parameter: double cg_gpnf = epsgpen

Parameter: double cg_epsi = 1.0e-1

Parameter: double cg_epsf = 1.0e-5

cg_scre states for Conjugate Gradient Stopping Criterion Relation, and cg_gpnf states for Conjugate Gradient Projected Gradient Final Norm. Both are related to a stopping criterion of Conjugate Gradients. This stopping criterion depends on the norm of the residual of the linear system. The norm of the residual should be less or equal than a small quantity which decreases as the iterate gets closer to the solution of the minimization problem. Then, the log of the required accuracy requested to Conjugate Gradient has a linear dependence on the log of the norm of the continuous projected gradient. This linear relation uses the squared Euclidian norm of the projected gradient if cg_scre is equal to 1 and uses the infinite norm if cg_scre is equal to 2. In addition, the precision required to CG is equal to cg_epsi (conjugate gradient initial epsilon) at the initial iterate and cg_epsf (conjugate gradient final epsilon) when the Euclidian- or infinite norm of the projected gradient is equal to cg_gpnf (conjugate gradients projected gradient final norm) which is an estimation of the value of the Euclidian- or infinite norm of the projected gradient at the solution. In case cg_scre is equal to 2, one suggests that cg_gpnf be equal to epsgpsn.

Parameter: double cg_epsnqmp = 1.0e-4

Parameter: size_t maxitnqmp = 5

Both parameters are used for a stopping criterion of the Conjugate Gradients subalgorithm. If the progress in the quadratic model is smaller than fraction epsnqmp of the best progress during maxitnqmp consecutive iterations then CG is stopped declaring "not enough progress of the quadratic model".

Parameter: int nearlyq = 0

Use nearlyq = 1 if the objective function is nearly quadratic. When an iteration of the CG finds a direction such that then, depending on nearlyq, CG does: if nearlyq=0, it stops at current point or if nearly=1 it takes the direction and tries to go to the boundary choosing the best among the two points at the boundary and the current one.

Parameter: double nint = 2.0

Constant for the interpolation. See the description of sigma1 and sigma2. Sometimes we take as a new trial step the previous one divided by nint.

Parameter: double next = 2.0

Constant for the extrapolation when extrapolating we try = \alpha} next.

Parameter: size_t mininterp = 4

Constant for testing if, after having made at least mininterp interpolations, the steplength is too small. In that case, failure of the line search is declared. It is possible that the direction is not a descent direction due to an error in the gradient calculations.

Parameter: size_t maxextrap = 100

Constant to limit the number of extrapolations in the Truncated Newton direction.

Parameter: int trtype = 0

Type of trust-region radius: trtype = 0 means Euclidian norm trust-region and trtype = 1 means infinite-norm trust-region.

Parameter: double eta = 0.9

Constant for deciding abandon the current face or not. We abandon the current face if the norm of the internal gradient (here, internal components of the continuous projected gradient) is smaller than (1-eta) times the norm of the continuous projected gradient. Using the default value is a rather conservative strategy in the sense that internal iterations are preferred over SPG iterations.

Parameter: double delmin = 0.1

Minimum "trust region" to compute the Truncated Newton direction.

Parameter: double lspgmi = 1.0e-10

Parameter: double lspgma = 1.0e+10

The spectral steplength, called , is projected inside the box [lspgmi,lspgma].

Parameter: double theta = 1.0e-6

Constant for the angle condition, i.e., at iteration we need a direction such that , where .

Parameter: double gamma = 1.0e-4

Constant for the Armijo condition.

Parameter: double beta = 0.5

Constant for the beta condition beta . If satisfies the Armijo condition but does not satisfy the beta condition then the point is accepted, but if it satisfied the Armijo condition and also satisfies the beta condition then we know that there is the possibility for a successful extrapolation.

Parameter: double sigma1 = 0.1

Parameter: double sigma2 = 0.9

Constants for the safeguarded interpolation. If \notin [sigma1, \sigma \alpha]}, then we take = \alpha/}nint.

Parameter: double epsrel = 1.0e-7

Parameter: double epsabs = 1.0e-10

Parameter: double infrel = 1.0e+20

Parameter: double infabs = 1.0e+99

These constants mean a "relative small number", "an absolute small number", "relative infinite number", "absolute infinite number", respectively.

8.3 Stopping Criteria

In the original paper, some criteria are used to detect if the iteration process should stop. They are (in the same order they appear)

• Test whether the Euclidean norm of the continuous projected gradient is small enough to declare convergence.

• Test whether the infinite norm of the continuous projected gradient is small enough to declare convergence.

• Test whether it was performed too many iterations without a satisfactory decreasing of the objective function value.

• Test whether it was performed too many iterations without a satisfactory decreasing of the Euclidean norm of the projected gradient.

The infinite norm of the projected gradient at the current iterate can be retrieved by calling ool_conmin_minimizer_size() function.

8.4 Example

See section 3. Quick Start, for an example program, replacing lines 73 and 75 of that code by

  const ool_conmin_minimizer_type *T = ool_conmin_minimizer_gencan;
  ool_conmin_gencan_parameters P;

The output of the program is shown below.

   0 : f( +0.000e+00, +0.000e+00, +0.000e+00, ... ) = +3.384e+03
   1 : f( +1.200e-01, +2.400e-01, +3.600e-01, ... ) = +1.170e+03
   2 : f( +1.000e-01, +2.000e-01, +3.000e-01, ... ) = +1.169e+03
   3 : f( +1.000e-01, +2.000e-01, +3.000e-01, ... ) = +1.168e+03

Convergence in 3 iterations
variables................:    100
function evaluations.....:     15
gradient evaluations.....:      5
function value...........:  1.167950e+03
projected gradient norm..:  0.000000e+00

8.5 References and Further Reading

• E.G. Birgin and J.M. Mart'{i}nez, Large-Scale Active-Set Box-Constrained Optimization Method with Spectral Projected Gradients, Computational Optimization and Applications, 23:101--125, 2002.

9. Tools

This chapter describes some extra frequently useful tools.

9.1 Numerical Gradient and Hessian

The functions described in this section are declared in the header file `ool_tools_diff.h'.

The numerical evaluation of the gradient and the Hessian can be done with the following functions.

Function: int ool_diff_g (double(* f) (const gsl_vector*, void*), gsl_vector * X, void * fparam, gsl_vector * G, const double eps)

This function numerically evaluates the gradient G of f at the point X. The derivatives are approximated by centered differences with step eps, i.e.,

df/dx_i (x) = ( f(x+eps e_i) - f(x-eps e_i) ) / ( 2 eps ) + O(eps^2)

where is the -th canonical vector. A suitable choice for eps is ||x||_{\infty}}, where states for the function evaluation accuracy. Typically, for near }, the machine roundoff, and } with order near 1, eps should be }.

Function: int ool_diff_g_auto (double(* f) (const gsl_vector*, void*), gsl_vector * X, void * fparam, gsl_vector * G)

This function numerically evaluates the gradient G of f at the point X, selecting the stepsize discretization automatically.

Function: int ool_diff_Hv (const ool_diff_Hv_accel * a, void(* df) (const gsl_vector*, void*, gsl_vector*), gsl_vector * X, void * fparam, const gsl_vector * V, gsl_vector * Hv, const double eps)

This function numerically evaluates the product Hv of the Hessian of f, at the point X, by a given vector V, which is numerically approximated by

d[H(x) v]_i = [ ( grad f(x+eps e_i) - grad f(x-eps e_i) ) / ( 2 eps ) ]^T v

The routine requires a function df that evaluates the gradient. Optionally, to speed up the numerical evaluation, we suggest to provide an accelerator a. If not provided, in case a receives NULL, the routine itself takes care of the required memory allocation and deallocation, each time it is called.

Function: ool_diff_Hv_accel * ool_diff_Hv_accel_alloc (size_t n)

This function returns a pointer to an accelerator object, which avoids memory allocations and deallocations, throughout the repetitive calls to function ool_diff_Hv.

Function: void ool_diff_Hv_accel_free (ool_diff_Hv_accel * a)

This routine frees memory associated to an accelerator object.

9.2 References and Further Reading

• C.T. Kelley, Iterative Methods for Optimization, Frontiers in Applied Mathematics, SIAM, Philadelphia, 1999.

A. Contributors to OOL

(See the AUTHORS file in the distribution for up-to-date information.)

Ricardo Biloti

Conceived OOL, wrote the design document. Wrote the codes for the SPG method and the numerical evaluation tools, as well as their documentation.

Luis Alberto D'Afonseca

Wrote all the codes in the C/GSL format. Wrote the CONMIN library.

Sergio Ventura

Wrote the documentation, as well as the html page. Converted GENCAN from Fortran 77 to C.

Iara da Cunha

Wrote the codes for the projected gradient method.

B. Reporting Constants

When writing numerical functions in a program which also uses OOL code you may find it convenient to adopt the same reporting conventions as in the library.

OOL_UNBOUNDEDF

Lower unbounded function.

OOL_INFEASIBLE

Infeasible point

OOL_FINNERIT

Too many inner iterations

OOL_FLSEARCH

Line search failed

OOL_FDDIR

Unable to find a descent direction

C. Autoconf Macros

For applications using autoconf the standard macro AC_CHECK_LIB can be used to link with the library automatically from a configure script. The library itself depends on the presence of a CBLAS and math library as well, so these must also be located before linking with the main libgsl file. The following commands should be placed in the `configure.in' file to perform these tests,

AC_CHECK_LIB(m,main)
AC_CHECK_LIB(gslcblas,main)
AC_CHECK_LIB(gsl,main)

checking for main in -lm... yes
checking for main in -lgslcblas... yes
checking for main in -lgsl... yes

The tests above will find any version of the library. They are suitable for general use, where the versions of the functions are not important. An alternative macro is available in the file `gsl.m4' to test for a specific version of the library. To use this macro simply add the following line to your `configure.in' file instead of the tests above:

AM_PATH_GSL(GSL_VERSION,
           [action-if-found],
           [action-if-not-found])

AC_MSG_ERROR(could not find required version of GSL)

libgsdv_la_LDFLAGS =    \
        $(GTK_LIBDIR) \
        $(GTK_LIBS) -lgsdvgsl $(GSL_LIBS) -lgslcblas

To test for inline the following test should be placed in your `configure.in' file,

AC_C_INLINE

if test "$ac_cv_c_inline" != no ; then
  AC_DEFINE(HAVE_INLINE,1)
  AC_SUBST(HAVE_INLINE)
fi

The following autoconf test will check for extern inline,

dnl Check for "extern inline", using a modified version
dnl of the test for AC_C_INLINE from acspecific.mt
dnl
AC_CACHE_CHECK([for extern inline], ac_cv_c_extern_inline,
[ac_cv_c_extern_inline=no
AC_TRY_COMPILE([extern $ac_cv_c_inline double foo(double x);
extern $ac_cv_c_inline double foo(double x) { return x+1.0; };
double foo (double x) { return x + 1.0; };], 
[  foo(1.0)  ],
[ac_cv_c_extern_inline="yes"])
])

if test "$ac_cv_c_extern_inline" != no ; then
  AC_DEFINE(HAVE_INLINE,1)
  AC_SUBST(HAVE_INLINE)
fi

The substitution of portability functions can be made automatically if you use autoconf. For example, to test whether the BSD function hypot is available you can include the following line in the configure file `configure.in' for your application,

AC_CHECK_FUNCS(hypot)

/* Substitute gsl_hypot for missing system hypot */

#ifndef HAVE_HYPOT
#define hypot gsl_hypot
#endif

Free Software Needs Free Documentation

The following article was written by Richard Stallman, founder of the GNU Project.

The biggest deficiency in the free software community today is not in the software--it is the lack of good free documentation that we can include with the free software. Many of our most important programs do not come with free reference manuals and free introductory texts. Documentation is an essential part of any software package; when an important free software package does not come with a free manual and a free tutorial, that is a major gap. We have many such gaps today.

Consider Perl, for instance. The tutorial manuals that people normally use are non-free. How did this come about? Because the authors of those manuals published them with restrictive terms--no copying, no modification, source files not available--which exclude them from the free software world.

That wasn't the first time this sort of thing happened, and it was far from the last. Many times we have heard a GNU user eagerly describe a manual that he is writing, his intended contribution to the community, only to learn that he had ruined everything by signing a publication contract to make it non-free.

Free documentation, like free software, is a matter of freedom, not price. The problem with the non-free manual is not that publishers charge a price for printed copies--that in itself is fine. (The Free Software Foundation sells printed copies of manuals, too.) The problem is the restrictions on the use of the manual. Free manuals are available in source code form, and give you permission to copy and modify. Non-free manuals do not allow this.

The criteria of freedom for a free manual are roughly the same as for free software. Redistribution (including the normal kinds of commercial redistribution) must be permitted, so that the manual can accompany every copy of the program, both on-line and on paper.

Permission for modification of the technical content is crucial too. When people modify the software, adding or changing features, if they are conscientious they will change the manual too--so they can provide accurate and clear documentation for the modified program. A manual that leaves you no choice but to write a new manual to document a changed version of the program is not really available to our community.

Some kinds of limits on the way modification is handled are acceptable. For example, requirements to preserve the original author's copyright notice, the distribution terms, or the list of authors, are ok. It is also no problem to require modified versions to include notice that they were modified. Even entire sections that may not be deleted or changed are acceptable, as long as they deal with nontechnical topics (like this one). These kinds of restrictions are acceptable because they don't obstruct the community's normal use of the manual.

However, it must be possible to modify all the technical content of the manual, and then distribute the result in all the usual media, through all the usual channels. Otherwise, the restrictions obstruct the use of the manual, it is not free, and we need another manual to replace it.

Please spread the word about this issue. Our community continues to lose manuals to proprietary publishing. If we spread the word that free software needs free reference manuals and free tutorials, perhaps the next person who wants to contribute by writing documentation will realize, before it is too late, that only free manuals contribute to the free software community.

If you are writing documentation, please insist on publishing it under the GNU Free Documentation License or another free documentation license. Remember that this decision requires your approval--you don't have to let the publisher decide. Some commercial publishers will use a free license if you insist, but they will not propose the option; it is up to you to raise the issue and say firmly that this is what you want. If the publisher you are dealing with refuses, please try other publishers. If you're not sure whether a proposed license is free, write to licensing@gnu.org.

You can encourage commercial publishers to sell more free, copylefted manuals and tutorials by buying them, and particularly by buying copies from the publishers that paid for their writing or for major improvements. Meanwhile, try to avoid buying non-free documentation at all. Check the distribution terms of a manual before you buy it, and insist that whoever seeks your business must respect your freedom. Check the history of the book, and try reward the publishers that have paid or pay the authors to work on it.

The Free Software Foundation maintains a list of free documentation published by other publishers, at http://www.fsf.org/doc/other-free-books.html.

GNU General Public License

Copyright © 1989, 1991 Free Software Foundation, Inc.
59 Temple Place - Suite 330, Boston, MA  02111-1307, USA

Everyone is permitted to copy and distribute verbatim copies of this
license document, but changing it is not allowed.

Preamble

The licenses for most software are designed to take away your freedom to share and change it. By contrast, the GNU General Public License is intended to guarantee your freedom to share and change free software--to make sure the software is free for all its users. This General Public License applies to most of the Free Software Foundation's software and to any other program whose authors commit to using it. (Some other Free Software Foundation software is covered by the GNU Library General Public License instead.) You can apply it to your programs, too.

When we speak of free software, we are referring to freedom, not price. Our General Public Licenses are designed to make sure that you have the freedom to distribute copies of free software (and charge for this service if you wish), that you receive source code or can get it if you want it, that you can change the software or use pieces of it in new free programs; and that you know you can do these things.

To protect your rights, we need to make restrictions that forbid anyone to deny you these rights or to ask you to surrender the rights. These restrictions translate to certain responsibilities for you if you distribute copies of the software, or if you modify it.

For example, if you distribute copies of such a program, whether gratis or for a fee, you must give the recipients all the rights that you have. You must make sure that they, too, receive or can get the source code. And you must show them these terms so they know their rights.

We protect your rights with two steps: (1) copyright the software, and (2) offer you this license which gives you legal permission to copy, distribute and/or modify the software.

Also, for each author's protection and ours, we want to make certain that everyone understands that there is no warranty for this free software. If the software is modified by someone else and passed on, we want its recipients to know that what they have is not the original, so that any problems introduced by others will not reflect on the original authors' reputations.

Finally, any free program is threatened constantly by software patents. We wish to avoid the danger that redistributors of a free program will individually obtain patent licenses, in effect making the program proprietary. To prevent this, we have made it clear that any patent must be licensed for everyone's free use or not licensed at all.

The precise terms and conditions for copying, distribution and modification follow.

1. This License applies to any program or other work which contains a notice placed by the copyright holder saying it may be distributed under the terms of this General Public License. The "Program", below, refers to any such program or work, and a "work based on the Program" means either the Program or any derivative work under copyright law: that is to say, a work containing the Program or a portion of it, either verbatim or with modifications and/or translated into another language. (Hereinafter, translation is included without limitation in the term "modification".) Each licensee is addressed as "you".

   Activities other than copying, distribution and modification are not covered by this License; they are outside its scope. The act of running the Program is not restricted, and the output from the Program is covered only if its contents constitute a work based on the Program (independent of having been made by running the Program). Whether that is true depends on what the Program does.

2. You may copy and distribute verbatim copies of the Program's source code as you receive it, in any medium, provided that you conspicuously and appropriately publish on each copy an appropriate copyright notice and disclaimer of warranty; keep intact all the notices that refer to this License and to the absence of any warranty; and give any other recipients of the Program a copy of this License along with the Program.

   You may charge a fee for the physical act of transferring a copy, and you may at your option offer warranty protection in exchange for a fee.

3. You may modify your copy or copies of the Program or any portion of it, thus forming a work based on the Program, and copy and distribute such modifications or work under the terms of Section 1 above, provided that you also meet all of these conditions:
   1. You must cause the modified files to carry prominent notices stating that you changed the files and the date of any change.

   2. You must cause any work that you distribute or publish, that in whole or in part contains or is derived from the Program or any part thereof, to be licensed as a whole at no charge to all third parties under the terms of this License.

   3. If the modified program normally reads commands interactively when run, you must cause it, when started running for such interactive use in the most ordinary way, to print or display an announcement including an appropriate copyright notice and a notice that there is no warranty (or else, saying that you provide a warranty) and that users may redistribute the program under these conditions, and telling the user how to view a copy of this License. (Exception: if the Program itself is interactive but does not normally print such an announcement, your work based on the Program is not required to print an announcement.)

   These requirements apply to the modified work as a whole. If identifiable sections of that work are not derived from the Program, and can be reasonably considered independent and separate works in themselves, then this License, and its terms, do not apply to those sections when you distribute them as separate works. But when you distribute the same sections as part of a whole which is a work based on the Program, the distribution of the whole must be on the terms of this License, whose permissions for other licensees extend to the entire whole, and thus to each and every part regardless of who wrote it.

   Thus, it is not the intent of this section to claim rights or contest your rights to work written entirely by you; rather, the intent is to exercise the right to control the distribution of derivative or collective works based on the Program.

   In addition, mere aggregation of another work not based on the Program with the Program (or with a work based on the Program) on a volume of a storage or distribution medium does not bring the other work under the scope of this License.

4. You may copy and distribute the Program (or a work based on it, under Section 2) in object code or executable form under the terms of Sections 1 and 2 above provided that you also do one of the following:
   1. Accompany it with the complete corresponding machine-readable source code, which must be distributed under the terms of Sections 1 and 2 above on a medium customarily used for software interchange; or,

   2. Accompany it with a written offer, valid for at least three years, to give any third party, for a charge no more than your cost of physically performing source distribution, a complete machine-readable copy of the corresponding source code, to be distributed under the terms of Sections 1 and 2 above on a medium customarily used for software interchange; or,

   3. Accompany it with the information you received as to the offer to distribute corresponding source code. (This alternative is allowed only for noncommercial distribution and only if you received the program in object code or executable form with such an offer, in accord with Subsection b above.)

   The source code for a work means the preferred form of the work for making modifications to it. For an executable work, complete source code means all the source code for all modules it contains, plus any associated interface definition files, plus the scripts used to control compilation and installation of the executable. However, as a special exception, the source code distributed need not include anything that is normally distributed (in either source or binary form) with the major components (compiler, kernel, and so on) of the operating system on which the executable runs, unless that component itself accompanies the executable.

   If distribution of executable or object code is made by offering access to copy from a designated place, then offering equivalent access to copy the source code from the same place counts as distribution of the source code, even though third parties are not compelled to copy the source along with the object code.

5. You may not copy, modify, sublicense, or distribute the Program except as expressly provided under this License. Any attempt otherwise to copy, modify, sublicense or distribute the Program is void, and will automatically terminate your rights under this License. However, parties who have received copies, or rights, from you under this License will not have their licenses terminated so long as such parties remain in full compliance.

6. You are not required to accept this License, since you have not signed it. However, nothing else grants you permission to modify or distribute the Program or its derivative works. These actions are prohibited by law if you do not accept this License. Therefore, by modifying or distributing the Program (or any work based on the Program), you indicate your acceptance of this License to do so, and all its terms and conditions for copying, distributing or modifying the Program or works based on it.

7. Each time you redistribute the Program (or any work based on the Program), the recipient automatically receives a license from the original licensor to copy, distribute or modify the Program subject to these terms and conditions. You may not impose any further restrictions on the recipients' exercise of the rights granted herein. You are not responsible for enforcing compliance by third parties to this License.

8. If, as a consequence of a court judgment or allegation of patent infringement or for any other reason (not limited to patent issues), conditions are imposed on you (whether by court order, agreement or otherwise) that contradict the conditions of this License, they do not excuse you from the conditions of this License. If you cannot distribute so as to satisfy simultaneously your obligations under this License and any other pertinent obligations, then as a consequence you may not distribute the Program at all. For example, if a patent license would not permit royalty-free redistribution of the Program by all those who receive copies directly or indirectly through you, then the only way you could satisfy both it and this License would be to refrain entirely from distribution of the Program.

   If any portion of this section is held invalid or unenforceable under any particular circumstance, the balance of the section is intended to apply and the section as a whole is intended to apply in other circumstances.

   It is not the purpose of this section to induce you to infringe any patents or other property right claims or to contest validity of any such claims; this section has the sole purpose of protecting the integrity of the free software distribution system, which is implemented by public license practices. Many people have made generous contributions to the wide range of software distributed through that system in reliance on consistent application of that system; it is up to the author/donor to decide if he or she is willing to distribute software through any other system and a licensee cannot impose that choice.

   This section is intended to make thoroughly clear what is believed to be a consequence of the rest of this License.

9. If the distribution and/or use of the Program is restricted in certain countries either by patents or by copyrighted interfaces, the original copyright holder who places the Program under this License may add an explicit geographical distribution limitation excluding those countries, so that distribution is permitted only in or among countries not thus excluded. In such case, this License incorporates the limitation as if written in the body of this License.

10. The Free Software Foundation may publish revised and/or new versions of the General Public License from time to time. Such new versions will be similar in spirit to the present version, but may differ in detail to address new problems or concerns.

    Each version is given a distinguishing version number. If the Program specifies a version number of this License which applies to it and "any later version", you have the option of following the terms and conditions either of that version or of any later version published by the Free Software Foundation. If the Program does not specify a version number of this License, you may choose any version ever published by the Free Software Foundation.

11. If you wish to incorporate parts of the Program into other free programs whose distribution conditions are different, write to the author to ask for permission. For software which is copyrighted by the Free Software Foundation, write to the Free Software Foundation; we sometimes make exceptions for this. Our decision will be guided by the two goals of preserving the free status of all derivatives of our free software and of promoting the sharing and reuse of software generally.
    NO WARRANTY

12. BECAUSE THE PROGRAM IS LICENSED FREE OF CHARGE, THERE IS NO WARRANTY FOR THE PROGRAM, TO THE EXTENT PERMITTED BY APPLICABLE LAW. EXCEPT WHEN OTHERWISE STATED IN WRITING THE COPYRIGHT HOLDERS AND/OR OTHER PARTIES PROVIDE THE PROGRAM "AS IS" WITHOUT WARRANTY OF ANY KIND, EITHER EXPRESSED OR IMPLIED, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE. THE ENTIRE RISK AS TO THE QUALITY AND PERFORMANCE OF THE PROGRAM IS WITH YOU. SHOULD THE PROGRAM PROVE DEFECTIVE, YOU ASSUME THE COST OF ALL NECESSARY SERVICING, REPAIR OR CORRECTION.

13. IN NO EVENT UNLESS REQUIRED BY APPLICABLE LAW OR AGREED TO IN WRITING WILL ANY COPYRIGHT HOLDER, OR ANY OTHER PARTY WHO MAY MODIFY AND/OR REDISTRIBUTE THE PROGRAM AS PERMITTED ABOVE, BE LIABLE TO YOU FOR DAMAGES, INCLUDING ANY GENERAL, SPECIAL, INCIDENTAL OR CONSEQUENTIAL DAMAGES ARISING OUT OF THE USE OR INABILITY TO USE THE PROGRAM (INCLUDING BUT NOT LIMITED TO LOSS OF DATA OR DATA BEING RENDERED INACCURATE OR LOSSES SUSTAINED BY YOU OR THIRD PARTIES OR A FAILURE OF THE PROGRAM TO OPERATE WITH ANY OTHER PROGRAMS), EVEN IF SUCH HOLDER OR OTHER PARTY HAS BEEN ADVISED OF THE POSSIBILITY OF SUCH DAMAGES.

Appendix: How to Apply These Terms to Your New Programs

If you develop a new program, and you want it to be of the greatest possible use to the public, the best way to achieve this is to make it free software which everyone can redistribute and change under these terms.

To do so, attach the following notices to the program. It is safest to attach them to the start of each source file to most effectively convey the exclusion of warranty; and each file should have at least the "copyright" line and a pointer to where the full notice is found.

one line to give the program's name and a brief idea of what it does.
Copyright (C) yyyy  name of author

This program is free software; you can redistribute it
and/or modify it under the terms of the GNU General Public
License as published by the Free Software Foundation; either
version 2 of the License, or (at your option) any later
version.

This program is distributed in the hope that it will be
useful, but WITHOUT ANY WARRANTY; without even the implied
warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR
PURPOSE.  See the GNU General Public License for more
details.

You should have received a copy of the GNU General Public
License along with this program; if not, write to the Free
Software Foundation, Inc., 59 Temple Place - Suite 330,
Boston, MA 02111-1307, USA.

Also add information on how to contact you by electronic and paper mail.

If the program is interactive, make it output a short notice like this when it starts in an interactive mode:

Gnomovision version 69, Copyright (C) 19yy name of author
Gnomovision comes with ABSOLUTELY NO WARRANTY; for details
type `show w'.  This is free software, and you are welcome
to redistribute it under certain conditions; type `show c'
for details.

The hypothetical commands `show w' and `show c' should show the appropriate parts of the General Public License. Of course, the commands you use may be called something other than `show w' and `show c'; they could even be mouse-clicks or menu items--whatever suits your program.

You should also get your employer (if you work as a programmer) or your school, if any, to sign a "copyright disclaimer" for the program, if necessary. Here is a sample; alter the names:

Yoyodyne, Inc., hereby disclaims all copyright interest in
the program `Gnomovision' (which makes passes at compilers)
written by James Hacker.

signature of Ty Coon, 1 April 1989
Ty Coon, President of Vice

This General Public License does not permit incorporating your program into proprietary programs. If your program is a subroutine library, you may consider it more useful to permit linking proprietary applications with the library. If this is what you want to do, use the GNU Library General Public License instead of this License.

GNU Free Documentation License

Copyright © 2000 Free Software Foundation, Inc.
59 Temple Place, Suite 330, Boston, MA  02111-1307, USA

Everyone is permitted to copy and distribute verbatim copies of this
license document, but changing it is not allowed.

1. PREAMBLE

   The purpose of this License is to make a manual, textbook, or other written document free in the sense of freedom: to assure everyone the effective freedom to copy and redistribute it, with or without modifying it, either commercially or noncommercially. Secondarily, this License preserves for the author and publisher a way to get credit for their work, while not being considered responsible for modifications made by others.

   This License is a kind of "copyleft", which means that derivative works of the document must themselves be free in the same sense. It complements the GNU General Public License, which is a copyleft license designed for free software.

   We have designed this License in order to use it for manuals for free software, because free software needs free documentation: a free program should come with manuals providing the same freedoms that the software does. But this License is not limited to software manuals; it can be used for any textual work, regardless of subject matter or whether it is published as a printed book. We recommend this License principally for works whose purpose is instruction or reference.

2. APPLICABILITY AND DEFINITIONS

   This License applies to any manual or other work that contains a notice placed by the copyright holder saying it can be distributed under the terms of this License. The "Document", below, refers to any such manual or work. Any member of the public is a licensee, and is addressed as "you".

   A "Modified Version" of the Document means any work containing the Document or a portion of it, either copied verbatim, or with modifications and/or translated into another language.

   A "Secondary Section" is a named appendix or a front-matter section of the Document that deals exclusively with the relationship of the publishers or authors of the Document to the Document's overall subject (or to related matters) and contains nothing that could fall directly within that overall subject. (For example, if the Document is in part a textbook of mathematics, a Secondary Section may not explain any mathematics.) The relationship could be a matter of historical connection with the subject or with related matters, or of legal, commercial, philosophical, ethical or political position regarding them.

   The "Invariant Sections" are certain Secondary Sections whose titles are designated, as being those of Invariant Sections, in the notice that says that the Document is released under this License.

   The "Cover Texts" are certain short passages of text that are listed, as Front-Cover Texts or Back-Cover Texts, in the notice that says that the Document is released under this License.

   A "Transparent" copy of the Document means a machine-readable copy, represented in a format whose specification is available to the general public, whose contents can be viewed and edited directly and straightforwardly with generic text editors or (for images composed of pixels) generic paint programs or (for drawings) some widely available drawing editor, and that is suitable for input to text formatters or for automatic translation to a variety of formats suitable for input to text formatters. A copy made in an otherwise Transparent file format whose markup has been designed to thwart or discourage subsequent modification by readers is not Transparent. A copy that is not "Transparent" is called "Opaque".

   Examples of suitable formats for Transparent copies include plain ASCII without markup, Texinfo input format, LaTeX input format, SGML or XML using a publicly available DTD, and standard-conforming simple HTML designed for human modification. Opaque formats include PostScript, PDF, proprietary formats that can be read and edited only by proprietary word processors, SGML or XML for which the DTD and/or processing tools are not generally available, and the machine-generated HTML produced by some word processors for output purposes only.

   The "Title Page" means, for a printed book, the title page itself, plus such following pages as are needed to hold, legibly, the material this License requires to appear in the title page. For works in formats which do not have any title page as such, "Title Page" means the text near the most prominent appearance of the work's title, preceding the beginning of the body of the text.

3. VERBATIM COPYING

   You may copy and distribute the Document in any medium, either commercially or noncommercially, provided that this License, the copyright notices, and the license notice saying this License applies to the Document are reproduced in all copies, and that you add no other conditions whatsoever to those of this License. You may not use technical measures to obstruct or control the reading or further copying of the copies you make or distribute. However, you may accept compensation in exchange for copies. If you distribute a large enough number of copies you must also follow the conditions in section 3.

   You may also lend copies, under the same conditions stated above, and you may publicly display copies.

4. COPYING IN QUANTITY

   If you publish printed copies of the Document numbering more than 100, and the Document's license notice requires Cover Texts, you must enclose the copies in covers that carry, clearly and legibly, all these Cover Texts: Front-Cover Texts on the front cover, and Back-Cover Texts on the back cover. Both covers must also clearly and legibly identify you as the publisher of these copies. The front cover must present the full title with all words of the title equally prominent and visible. You may add other material on the covers in addition. Copying with changes limited to the covers, as long as they preserve the title of the Document and satisfy these conditions, can be treated as verbatim copying in other respects.

   If the required texts for either cover are too voluminous to fit legibly, you should put the first ones listed (as many as fit reasonably) on the actual cover, and continue the rest onto adjacent pages.

   If you publish or distribute Opaque copies of the Document numbering more than 100, you must either include a machine-readable Transparent copy along with each Opaque copy, or state in or with each Opaque copy a publicly-accessible computer-network location containing a complete Transparent copy of the Document, free of added material, which the general network-using public has access to download anonymously at no charge using public-standard network protocols. If you use the latter option, you must take reasonably prudent steps, when you begin distribution of Opaque copies in quantity, to ensure that this Transparent copy will remain thus accessible at the stated location until at least one year after the last time you distribute an Opaque copy (directly or through your agents or retailers) of that edition to the public.

   It is requested, but not required, that you contact the authors of the Document well before redistributing any large number of copies, to give them a chance to provide you with an updated version of the Document.

5. MODIFICATIONS

   You may copy and distribute a Modified Version of the Document under the conditions of sections 2 and 3 above, provided that you release the Modified Version under precisely this License, with the Modified Version filling the role of the Document, thus licensing distribution and modification of the Modified Version to whoever possesses a copy of it. In addition, you must do these things in the Modified Version:

   1. Use in the Title Page (and on the covers, if any) a title distinct from that of the Document, and from those of previous versions (which should, if there were any, be listed in the History section of the Document). You may use the same title as a previous version if the original publisher of that version gives permission.

   2. List on the Title Page, as authors, one or more persons or entities responsible for authorship of the modifications in the Modified Version, together with at least five of the principal authors of the Document (all of its principal authors, if it has less than five).

   3. State on the Title page the name of the publisher of the Modified Version, as the publisher.

   4. Preserve all the copyright notices of the Document.

   5. Add an appropriate copyright notice for your modifications adjacent to the other copyright notices.

   6. Include, immediately after the copyright notices, a license notice giving the public permission to use the Modified Version under the terms of this License, in the form shown in the Addendum below.

   7. Preserve in that license notice the full lists of Invariant Sections and required Cover Texts given in the Document's license notice.

   8. Include an unaltered copy of this License.

   9. Preserve the section entitled "History", and its title, and add to it an item stating at least the title, year, new authors, and publisher of the Modified Version as given on the Title Page. If there is no section entitled "History" in the Document, create one stating the title, year, authors, and publisher of the Document as given on its Title Page, then add an item describing the Modified Version as stated in the previous sentence.

   10. Preserve the network location, if any, given in the Document for public access to a Transparent copy of the Document, and likewise the network locations given in the Document for previous versions it was based on. These may be placed in the "History" section. You may omit a network location for a work that was published at least four years before the Document itself, or if the original publisher of the version it refers to gives permission.

   11. In any section entitled "Acknowledgments" or "Dedications", preserve the section's title, and preserve in the section all the substance and tone of each of the contributor acknowledgments and/or dedications given therein.

   12. Preserve all the Invariant Sections of the Document, unaltered in their text and in their titles. Section numbers or the equivalent are not considered part of the section titles.

   13. Delete any section entitled "Endorsements". Such a section may not be included in the Modified Version.

   14. Do not retitle any existing section as "Endorsements" or to conflict in title with any Invariant Section.

   If the Modified Version includes new front-matter sections or appendices that qualify as Secondary Sections and contain no material copied from the Document, you may at your option designate some or all of these sections as invariant. To do this, add their titles to the list of Invariant Sections in the Modified Version's license notice. These titles must be distinct from any other section titles.

   You may add a section entitled "Endorsements", provided it contains nothing but endorsements of your Modified Version by various parties--for example, statements of peer review or that the text has been approved by an organization as the authoritative definition of a standard.

   You may add a passage of up to five words as a Front-Cover Text, and a passage of up to 25 words as a Back-Cover Text, to the end of the list of Cover Texts in the Modified Version. Only one passage of Front-Cover Text and one of Back-Cover Text may be added by (or through arrangements made by) any one entity. If the Document already includes a cover text for the same cover, previously added by you or by arrangement made by the same entity you are acting on behalf of, you may not add another; but you may replace the old one, on explicit permission from the previous publisher that added the old one.

   The author(s) and publisher(s) of the Document do not by this License give permission to use their names for publicity for or to assert or imply endorsement of any Modified Version.

6. COMBINING DOCUMENTS

   You may combine the Document with other documents released under this License, under the terms defined in section 4 above for modified versions, provided that you include in the combination all of the Invariant Sections of all of the original documents, unmodified, and list them all as Invariant Sections of your combined work in its license notice.

   The combined work need only contain one copy of this License, and multiple identical Invariant Sections may be replaced with a single copy. If there are multiple Invariant Sections with the same name but different contents, make the title of each such section unique by adding at the end of it, in parentheses, the name of the original author or publisher of that section if known, or else a unique number. Make the same adjustment to the section titles in the list of Invariant Sections in the license notice of the combined work.

   In the combination, you must combine any sections entitled "History" in the various original documents, forming one section entitled "History"; likewise combine any sections entitled "Acknowledgments", and any sections entitled "Dedications". You must delete all sections entitled "Endorsements."

7. COLLECTIONS OF DOCUMENTS

   You may make a collection consisting of the Document and other documents released under this License, and replace the individual copies of this License in the various documents with a single copy that is included in the collection, provided that you follow the rules of this License for verbatim copying of each of the documents in all other respects.

   You may extract a single document from such a collection, and distribute it individually under this License, provided you insert a copy of this License into the extracted document, and follow this License in all other respects regarding verbatim copying of that document.

8. AGGREGATION WITH INDEPENDENT WORKS

   A compilation of the Document or its derivatives with other separate and independent documents or works, in or on a volume of a storage or distribution medium, does not as a whole count as a Modified Version of the Document, provided no compilation copyright is claimed for the compilation. Such a compilation is called an "aggregate", and this License does not apply to the other self-contained works thus compiled with the Document, on account of their being thus compiled, if they are not themselves derivative works of the Document.

   If the Cover Text requirement of section 3 is applicable to these copies of the Document, then if the Document is less than one quarter of the entire aggregate, the Document's Cover Texts may be placed on covers that surround only the Document within the aggregate. Otherwise they must appear on covers around the whole aggregate.

9. TRANSLATION

   Translation is considered a kind of modification, so you may distribute translations of the Document under the terms of section 4. Replacing Invariant Sections with translations requires special permission from their copyright holders, but you may include translations of some or all Invariant Sections in addition to the original versions of these Invariant Sections. You may include a translation of this License provided that you also include the original English version of this License. In case of a disagreement between the translation and the original English version of this License, the original English version will prevail.

10. TERMINATION

    You may not copy, modify, sublicense, or distribute the Document except as expressly provided for under this License. Any other attempt to copy, modify, sublicense or distribute the Document is void, and will automatically terminate your rights under this License. However, parties who have received copies, or rights, from you under this License will not have their licenses terminated so long as such parties remain in full compliance.

11. FUTURE REVISIONS OF THIS LICENSE

    The Free Software Foundation may publish new, revised versions of the GNU Free Documentation License from time to time. Such new versions will be similar in spirit to the present version, but may differ in detail to address new problems or concerns. See http://www.gnu.org/copyleft/.

    Each version of the License is given a distinguishing version number. If the Document specifies that a particular numbered version of this License "or any later version" applies to it, you have the option of following the terms and conditions either of that specified version or of any later version that has been published (not as a draft) by the Free Software Foundation. If the Document does not specify a version number of this License, you may choose any version ever published (not as a draft) by the Free Software Foundation.

ADDENDUM: How to use this License for your documents

To use this License in a document you have written, include a copy of the License in the document and put the following copyright and license notices just after the title page:

  Copyright (C) year your name.  Permission is
  granted to copy, distribute and/or modify this document
  under the terms of the GNU Free Documentation License,
  Version 1.1 or any later version published by the Free
  Software Foundation; with the Invariant Sections being
  list their titles, with the Front-Cover Texts being
  list, and with the Back-Cover Texts being
  list.  A copy of the license is included in the
  section entitled ``GNU Free Documentation License''.

If you have no Invariant Sections, write "with no Invariant Sections" instead of saying which ones are invariant. If you have no Front-Cover Texts, write "no Front-Cover Texts" instead of "Front-Cover Texts being list"; likewise for Back-Cover Texts.

If your document contains nontrivial examples of program code, we recommend releasing these examples in parallel under your choice of free software license, such as the GNU General Public License, to permit their use in free software.

Function Index

Parameter Index

Type Index

Concept Index

Table of Contents

1. Introduction

1.1 Routines available in OOL
1.2 OOL is Free Software
1.3 Obtaining OOL
1.4 No Warranty
1.5 Reporting Bugs

2. Using the library

2.1 ANSI C Compliance
2.2 Compiling and Linking
2.3 Shared Libraries
2.4 Compatibility with C++
2.5 Aliasing of arrays
2.6 Thread-safety

3. Quick Start

3.1 Example

4. Brief Theoretical Introduction

4.1 Theory Overview
4.2 Optimality Conditions

4.2.1 Convex Case
4.2.2 Box Constraints

4.3 General Method Structure

4.3.1 Line Search

4.4 References and Further Reading

5. Constrained Optimization

5.1 Choosing the Minimization Method
5.2 Initialization and Finalization
5.3 Providing a function to minimize
5.4 Providing the constraints
5.5 Iteration
5.6 Stopping Criteria
5.7 Algorithms
5.8 References and Further Reading

6. Projected Gradient Method

6.1 Overview
6.2 Parameters
6.3 Stopping Criteria
6.4 Example
6.5 References and Further Reading

7. Spectral Projected Gradient Method

7.1 Overview
7.2 Parameters
7.3 Stopping Criteria
7.4 Example
7.5 References and Further Reading

8. Gencan Method

8.1 Overview
8.2 Parameters
8.3 Stopping Criteria
8.4 Example
8.5 References and Further Reading

9. Tools

9.1 Numerical Gradient and Hessian
9.2 References and Further Reading

A. Contributors to OOL
B. Reporting Constants
C. Autoconf Macros
Free Software Needs Free Documentation
GNU General Public License

Preamble
Appendix: How to Apply These Terms to Your New Programs

GNU Free Documentation License

ADDENDUM: How to use this License for your documents

Function Index
Parameter Index
Type Index
Concept Index

Short Table of Contents

1. Introduction
2. Using the library
3. Quick Start
4. Brief Theoretical Introduction
5. Constrained Optimization
6. Projected Gradient Method
7. Spectral Projected Gradient Method
8. Gencan Method
9. Tools
A. Contributors to OOL
B. Reporting Constants
C. Autoconf Macros
Free Software Needs Free Documentation
GNU General Public License
GNU Free Documentation License
Function Index
Parameter Index
Type Index
Concept Index

About this document

where the Example assumes that the current position is at Subsubsection One-Two-Three of a document of the following structure:

• 1. Section One
  • 1.1 Subsection One-One
    • ...
  • 1.2 Subsection One-Two
    • 1.2.1 Subsubsection One-Two-One
    • 1.2.2 Subsubsection One-Two-Two
    • 1.2.3 Subsubsection One-Two-Three     <== Current Position
    • 1.2.4 Subsubsection One-Two-Four
  • 1.3 Subsection One-Three
    • ...
  • 1.4 Subsection One-Four